Possibly the most famous electronic music patent ever, this is
the guts of the circuitry for the Moog 904A voltage-controlled
low-pass filter, the Moog 904B voltage-controlled high-pass
filter and the Moog 904C filter coupler. And all later
Moog VCFs are based on the 904A.
This filter is certainly well known for its characteristic
sound, but I want to point out some of the breakthrough
concepts behind it.
First, voltage-tuning a filter over a wide range is a difficult
electrical engineering problem. How do you do it?
Electrical circuits don't normally work that way. Bob Moog
looked to the emitter resistance of balanced pairs of
transistors -- the emitter resistance can be varied
exponentially over a wide range and the symmetry of the balanced
circuit cancels out most of the control signal and even-order
harmonic distortion.
Bob Moog probably noted that a filter for musical applications
should have a steep slope (24 dB/oct in this case), should have
the resonance adjustable without affecting the tuned frequency
(and vice-versa), and that the resonance should be adjustable to
oscillation. The
four-single-pole-low-pass-sections-with-feedback approach was not
typically used for filter designs at the time, but it addresses
these issues perfectly. (For comparison, the peaking
frequency for the traditional 2-pole biquad filter is not the same
as the filter's tuned frequency, although the two approach each
other toward oscillation.)
And because the filter can be run at or near oscillation, it
will likely be used that way patched with 1 volt/octave
voltage-controlled oscillators. So it is important that
the tuning of the VCF accurately track the tuning of the VCO.
![[Moog 904A module]](images/mod904a.jpeg) The transfer functions of the low-pass and high-pass filters are:
The transfer functions of the low-pass and high-pass filters are:
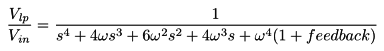
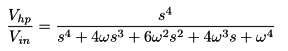
Where
Vlp is the low-pass filter output
Vhp is the high-pass filter output
ω is the filter's tuned frequency
s is the complex frequency
feedback is the fraction of negative feedback
applied, a value from 0.0 (no resonance) to 4.0 (for
oscillation)
Without feedback, all four poles are real and sit on top of each
other at x = -ω. As
feedback is applied, the four poles split out, literally in the
shape of an "X" and move apart 90o from each
other. At a feedback factor of 4.0 the two rightmost poles
hit the the y axis and the filter oscillates.
Bob Moog's design does all this with a remarkably simple
circuit that performs well, and any inaccuracies it
does have provide a lot of character to the sound. (The
filter can be overdriven in a musically pleasing way as all
the transistor stages clip gradually.)
![[Moog 904b module]](images/mod904b.jpeg) So this is a killer design from many angles.
So this is a killer design from many angles.
The 904B high-pass filter is the electrical brother of the
low-pass filter, although the schematics look very different
from a distance. The high-pass filter does not have a
feedback path and thus no resonance control; perhaps there are
stability issues here. (On the other hand, the Moog AES
article below mentions employing a small amount of feedback to
sharpen up the response curve.)
![[Moog 904C module]](images/mod904c.jpeg) The 904C filter coupler is the obvious way of doubling up a
low-pass VCF and a high-pass VCF in series for a bandpass filter
or in parallel for a band reject filter with individual controls
of center frequency and bandwidth. The advantage here is
that the bandwidth control voltage is calibrated in
volts/octave, again something you won't see in more traditional
filters.
The 904C filter coupler is the obvious way of doubling up a
low-pass VCF and a high-pass VCF in series for a bandpass filter
or in parallel for a band reject filter with individual controls
of center frequency and bandwidth. The advantage here is
that the bandwidth control voltage is calibrated in
volts/octave, again something you won't see in more traditional
filters.
Roland and other companies have produced diode ladder filters
using diodes as the tuning elements instead of transistors,
presumably as a "way around the patent". The diodes do not
separate the capacitor sections from each other like the
transistors do, so the diode-based ladder filters have their
poles scattered along the x axis instead of all at the same
location. They sound different, their cutoff slope is much
more gradual, and they require a lot more feedback to oscillate.
![[patent thumbnail]](images/US03475623.gif)
![[Moog 904A module]](images/mod904a.jpeg) The transfer functions of the low-pass and high-pass filters are:
The transfer functions of the low-pass and high-pass filters are:
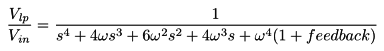
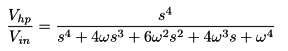
![[Moog 904b module]](images/mod904b.jpeg) So this is a killer design from many angles.
So this is a killer design from many angles.
![[Moog 904C module]](images/mod904c.jpeg) The 904C filter coupler is the obvious way of doubling up a
low-pass VCF and a high-pass VCF in series for a bandpass filter
or in parallel for a band reject filter with individual controls
of center frequency and bandwidth. The advantage here is
that the bandwidth control voltage is calibrated in
volts/octave, again something you won't see in more traditional
filters.
The 904C filter coupler is the obvious way of doubling up a
low-pass VCF and a high-pass VCF in series for a bandpass filter
or in parallel for a band reject filter with individual controls
of center frequency and bandwidth. The advantage here is
that the bandwidth control voltage is calibrated in
volts/octave, again something you won't see in more traditional
filters.
![[patent thumbnail]](images/US03800088.gif)
![[Moog 1630 module]](images/mod1630.jpeg) The basic idea is an implementation of the trigonometric
identity for the cosine of the sum of two angles to shift the
frequency up:
The basic idea is an implementation of the trigonometric
identity for the cosine of the sum of two angles to shift the
frequency up:
![[patent thumbnail]](images/US03943456.gif)
![[Crumar Spirit]](images/crumar-spirit.jpeg) This wasn't used in any Moog product, but it was used for the
second LFO ("Shaper Y") in the Crumar Spririt synthesizer
designed by Bob Moog, Jim Scott and Tom Rhea and released in
1983.
This wasn't used in any Moog product, but it was used for the
second LFO ("Shaper Y") in the Crumar Spririt synthesizer
designed by Bob Moog, Jim Scott and Tom Rhea and released in
1983.
![[patent thumbnail]](images/US03974461.gif)
![[patent thumbnail]](images/US03981218.gif)
![[patent thumbnail]](images/US03991645.gif)
![[patent thumbnail]](images/US04046049.gif)
![[patent thumbnail]](images/US03997863.gif)
![[patent thumbnail]](images/US04027569.gif)
![[patent thumbnail]](images/US04028979.gif)
![[patent thumbnail]](images/US04032720.gif)
![[patent thumbnail]](images/US04038898.gif)
![[patent thumbnail]](images/US04050343.gif)
![[MinitMoog, Moog Satellite]](images/minitmoog.jpeg) This is the patent for the MinitMoog and Moog Satellite preset
synths. These are something like the Arp Soloist; 13 preset
sounds where each preset controls 12 parameters through a
resistor matrix. 1 LFO, 1 VCO, 1 BP VCF, 1 LP VCF, 1
VCA. (The MinitMoog has a second VCO, literally
piggybacked on the circuit board.)
This is the patent for the MinitMoog and Moog Satellite preset
synths. These are something like the Arp Soloist; 13 preset
sounds where each preset controls 12 parameters through a
resistor matrix. 1 LFO, 1 VCO, 1 BP VCF, 1 LP VCF, 1
VCA. (The MinitMoog has a second VCO, literally
piggybacked on the circuit board.)
![[patent thumbnail]](images/US04099439.gif)
![[patent thumbnail]](images/US04145943.gif)
![[patent thumbnail]](images/US04228717.gif)
![[PolyMoog]](images/polymoog.jpeg)
![[patent thumbnail]](images/US04108041.gif)
![[patent thumbnail]](images/US04117413.gif)
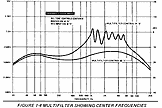 Here is a plot from the Technical Service Manual for the Moog
Lab Series Amplifiers (Norlin Music).
Here is a plot from the Technical Service Manual for the Moog
Lab Series Amplifiers (Norlin Music).
![[patent thumbnail]](images/US04158751.gif)
![[Moog/Bode Vocoder]](images/vocoder.jpeg) This is the patent for the Moog 16-channel Vocoder.
This is the patent for the Moog 16-channel Vocoder.
![[patent thumbnail]](images/US04166197.gif)
![[patent thumbnail]](images/US04180707.gif)
![[patent thumbnail]](images/US04202238.gif)
![[patent thumbnail]](images/US04213367.gif)
![[patent thumbnail]](images/US04280387.gif)
![[patent thumbnail]](images/US04282787.gif)
![[patent thumbnail]](images/US04778951.gif)