Nonlinearities in Vacuum Tubes, Bipolar Transistors, and Field-Effect Transistors

J. Donald Tillman
Sept 2024

Abstract: The three main types of active devices used in audio are examined; vacuum tubes, bipolar junction transistors, and field effect transistors. While the underlying physics and operation of these devices are wildly different, an analysis reveals that, under practical conditions, their distortion products are found to be very similar, and almost entirely 2nd harmonic distortion.

One of the enduring bits of audio folklore is the story that vacuum tubes create even-order harmonic distortion products, while transistors create odd-order harmonic distortion products. And that even harmonics are good while odd harmonics are bad.

Of course so much depends on the specific circuit topologies, the various circuit components and values, operating voltages and currents, local feedback, and the input and output situations. And there are multiple stages involved. But this discussion will target the nonlinearities that are germain to the devices themselves.

A Quick Review of the Devices

We have three types of active devices suitable for any kind of audio work: vacuum tubes, bipolar transistors, and field-effect transistors. They have a lot in common; a current flows between two terminals, controlled by a third terminal. They are used in similar ways, and in similar circuit topologies. However, the specific physics of their operation varies wildly, and their terminals have different names.

Vacuum tubes were first available in the 1920s, and were the sole amplification device until transistors. In operation, a heated cathode gives off electrons flowing to a positive plate. There is a wire grid placed between them that can close off the electron flow with a voltage that is negative with respect to the cathode.

While the triode has a single grid, there are also variations with additional grids, the tetrode and the pentode, but the physics is the same.

Unlike transistors, vacuum tubes are only available in one polarity, which limits the available circuit configurations.

Vacuum tube

Bipolar transistors were first available in the 1950s. The current into a thin slice of a pn junction, from the base terminal to the emitter terminal, is a small fraction of the current that flows from the collector terminal to the emitter terminal.

The bipolar transistor is a basically a current input / current output device.

Bipolar transistor

Field effect transistors were first available in the 1960s. Current flows from the drain terminal to the source terminal through a piece of silicon, and is controlled by an electric field present from the voltage at the gate terminal. There are a number of variations.

Field-effect transistor

All three types of devices can be configured in three different ways, depending upon which pin is "common", or neither input nor output.

Common cathode/emitter/source for amplification, where the input signal controls the output current.
Common grid/base/gate passes the current straight through from input to output, and as a side effect transforms a low impedance into a high impedance.
Common plate/collector/drain where any difference between the input and the output voltage is used to drive the output to mimimize the difference, effectively buffering the input signal. This is also called a cathode/emitter/source follower circuit, as the output voltage follows the input voltage with a voltage gain near unity over a wide range of loads.

For this article we are only going to consider the first configuration, for amplification.

Harmonic Distortion is Cosine-Aligned

"Harmonic Distortion" has traditionally been a measure of the quality of an amplifier, or other audio device, with respect to its linearity. The ratio of the output voltage to the input voltage should be a constant value. And if you plot the output-vs-input on an XY plot you should see a perfectly straight line. And any curve, wiggle, warp or other deviation from that that line would be a nonlinearity.

The procedure to measure harmonic distortion is to use the purest available source of a sine wave, apply it to the input at the intended level, and measure the output signal. Any nonlinearities will show up in the output as a misshapen sine wave, which would have additional harmonic content. The harmonic distortion is the percentage of the extraneous harmonic content in the output signal.

The "Total Harmonic Distortion", or THD, measurement is calculated as the square root of the sum of the squares of the levels of the individual harmonics.

When a sine wave feeds a simple nonlinear function, the trip up the curve will be the same as the trip back down the curve. This symmetry means that the harmonics will all have to be cosine-aligned (or negative cosine-aligned) with the fundamental. An analysis that starts with a cosine wave will result in a series of cosine waves, while an analysis that starts with a sine wae will get more complicated.

Here we have our input sine wave, and the 2nd through 9th harmonics, all phase-aligned to the positive peak.

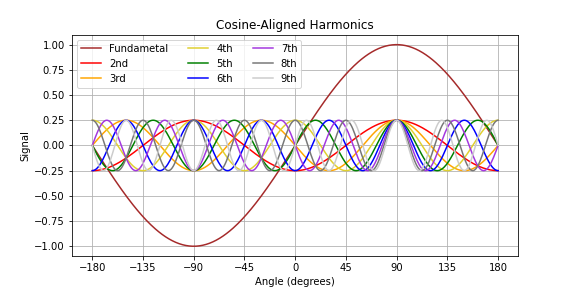
We can see odd harmonics will line up in the same direction as the peaks, while even harmonics will line up opposite those peaks.

If we split out the odd and even harmonics, we can see that the odd harmonics will run in the direction of the alternate half cycles of fundamental, while the even harmonics will run with and against the fundamental on alternate half cycles.

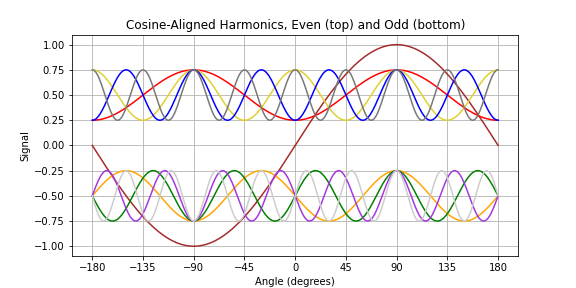
More subtly, even harmonics will not cross zero with the fundamental sine, but the odd harmonics always will. That makes sense, as a DC bias could be considered an even harmonic (the 0th harmonic).

Bipolar Transistors

Bipolar transistors are easily the most popular active devices in the analog world. And transistor amplifiers are primarily responsible for the tube/transistor debate.

Bipolar transistors are basically current input / current output devices. In comparison, vacuum tubes and FETs which are voltage input / current output devices and draw neglidgible input current under normal operating conditions.

In a common-emitter configuration, with an input current source applied to the base and an output current from the collector, a bipolar transistor is almost perfectly linear. The current gain lies roughly between 50 and 200, and can vary with the transistor model, the temperature, and manufacturing inconsistencies.

$$ i_C = \beta \: i_B + I_{CEO} $$

Where:

$i_C$ is the output collector current, $\beta$ is the current gain of the transistor, $i_B$ is the input base current, and $I_{CEO}$ is the collector cutoff current, a leakage.

More typically we are interested in a voltage gain situation, and so a voltage is applied to the base, and a load resistor converts the collector current into an output voltage. The emitter-base diode has a log current-to-voltage characterstic, and thus an exponential voltage-to-current characteristic, and the result is an exponential relationship between the base-emitter voltage and the collector current. According to the Ebers-Moll model:

$$ I_C = \alpha_{F} \; I_{ES} ( e^{\textstyle \frac{V_{BE}}{V_T}} - 1) $$

Where:

$I_C$ is the output collector current, $\alpha_F$ is common-base current gain, typically 0.99, $I_{ES}$ is the reverse saturation current, $V_{BE}$ is the base-emitter voltage, $V_T$ is the thermal voltage, $kT/q$, typically 0.6 Volts, $k$ is Boltzman's consant, $T$ is the temperature in degrees Kelvin, and $q$ is the charge on an electron.

There are a lot of application dependent variables here, as expected, the input signal level, the bias, and the output signal level can all be scaled and adjusted for the situation. But the sole nonlinearity is the exponential function. And as an aside, the exponential function can hold remarkable well in practice if care is taken with respect to temperature and a holding the collector-to-base voltage fixed.

To compare nonlinearities we will need to abstract them from the circuit and normalize them. So for a bipolar transistor, the nonlinearity can be considered:

$$ V_{OUT} = e^{\textstyle a V_{IN}}$$

Where:

$V_{IN}$ is the input voltage, normalized as a +/- 1.0 V sine wave, $a$ is a gain factor, and the result is the output voltage.

The effect of that nonlinearity is going to be dependent on the signal level.

In my previous artice, I introduced a triptych display to plot the nonlinear transfer function curve, the distorted sine waveform, and the distortion spectrum, all together. It can be enlightening to see a mechanism from multiple angles at the same time. In order to compare nonlinearities, the transfer function is displayed normalized to a ± 1.0 Volt input, a ± 1.0 Volt output, and a positive polarity.

I usually start with a 10% THD, certainly arbirary and higher than normal, to demonstrate the differences between the curves more clearly. For a 10% THD level, the value of $a$ in the equation above above is 0.4

Here is a triptych display for the exponential nonlinearithy of the bipolar transistor:

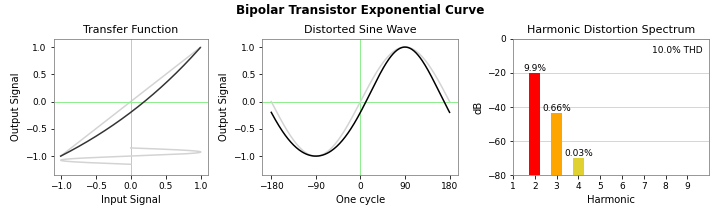
(Note that Total Harmonic Distortion is calculated as an RMS value, the square root of the sum of the squares of the individual harmonic levels, and not a simple sum.)

So that is almost entirely 2nd harmonic distortion. The third harmonic is down over 20dB below the 2nd harmonic, which is already 20dB below the fundamental. And the 4th harmonic is barely there. The harmonic content is dropping off very quickly, far faster than you would expect to see from, say, a filter.

The next step is to see how the harmonic distortion spectrum changes with signal level. That plot is here:

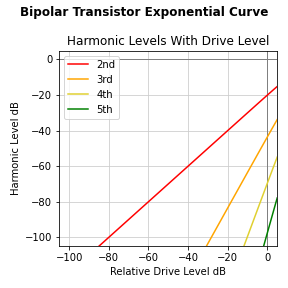
bipolar transistor distortion with level

These curves show the levels of the harmonic distortion components dropping steadily with the input signal level. The 2nd harmonic level is directly proportional to signal level, and the higher harmonics drop faster.

Note that this contradicts the folklore of transistors producing odd harmonic distortion. If we drive a transistor stage to, say, 1% distortion, the 3rd harmonic contribution will be less than 1% of that 1% distortion.

Field Effect Transistors

There are a number of variations of Field Effect Transistors but the physics of the mechanisms are similar.

An FET has two distinct regions of operation; the "ohmic" or "triode" region at low drain-to-source voltages where it acts as a variable resistor, and the "saturation" region at higher drain-to-source voltages, where it acts as a current source. For normal voltage gain operation the unit will be running in the saturation region. It is certainly possible to bump into the ohmic region on peaks, but that would be an implementation detail.

(As a side note, I will point out that in FET terminology "pinch-off voltage" has multiple conflicting interpretations, which is confusing, with similar values, which makes it even more confusing. I will avoid the term here, other than to point out that the "saturation region" is also called the "pinch-off region", which makes it more confusing still. Oh, and the term "saturation region" has the opposite meaning for bipolar transistors and FETs.)

For an N-channel junction FET operating in the saturation region the equation for the drain current is:

$$\begin{eqnarray} I_{DS} &=& I_{DSS} ( 1 - V_{GS} / V_{GS(off)})^2 &\text{, for}& V_{GS} \ge V_{GS(off)} \\ &=& 0 &\text{, for}& V_{GS} \lt V_{GS(off)} \end{eqnarray}$$

Where:

$I_{DS}$ is the output drain current in the saturation region of operation, $V_{GS}$ is the gate to source voltage, $V_{GS(off)}$ is the gate-to-source cutoff voltage device parameter, and $I_{DSS}$ is the gate-shorted drain current device parameter.

While the physics gives us a squaring operation, there is no intent to operate on the left side of the parabola. So the value of $I_{DS}$ is zero when $V_{GS}$ is less than $V_{GS(off)}$.

Additionally, the gate-source diode should not be conducting, so $V_{GS}$ should be less than +0.5 volts.

MOSFET transistors are very similar, with a similar transfer function, but the equation ends up being different because MOSFETs specify different device parameters.

$$\begin{eqnarray} I_{DS} &=& g_{fs} ( V_{GS} - V_{th})^2 &\text{, for}& V_{GS} \ge V_{th} \\ &=& 0 &\text{, for}& V_{GS} \lt V_{th} \end{eqnarray}$$

Where:

$I_{DS}$ is the output drain current in the saturation region of operation, $V_{GS}$ is the gate to source voltage, $g_{fs}$ is the transconductance device parameter, $V_{th}$ is the gate threshold voltage device parameter.

Again, there is no intention of operating on the left side of the parabola, so the value of $I_{DS}$ is zero when $V_{GS}$ is less than $V_{th}$.

We can abstract out a transfer function applicable to both JFET and MOSFET dervices as:

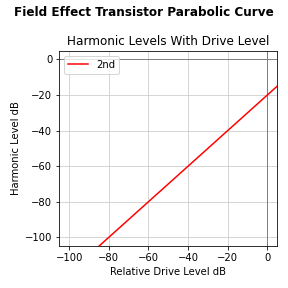
$$v_{out} = (v_{in} + 1)^2$$

Where:

$v_{out}$ is the output signal, and $v_{in}$ is the input signal, 1 Vp-p maximum.

And here is a triptych display for the parabolic nonlinearity of field-effect transistors:

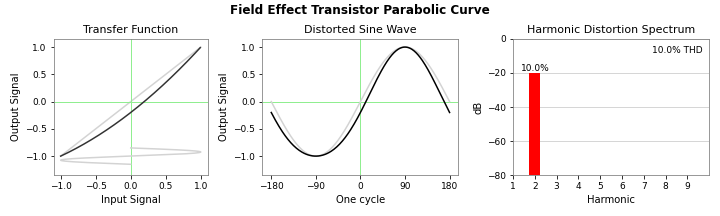
Square law distortion is so simple that we don't even need to use a Fourier Transform to see the distortion generated products. Just expand the square term and apply a trigonometric identity:

$$v_{in} = a \cos(x)$$ $$v_{out} = (a \cos(x) + 1 )^2$$ $$v_{out} = a^2 \cos^2(x) + 2 a \cos(x) + 1$$

Trig identity:

$$ \cos(2 x) = 2 \cos^2(x) - 1 $$ $$ v_{out} = a^2 \frac{\cos(2x) + 1}{2} + 2 a \cos(x) + 1$$

Ignoring DC:

$$ v_{out} = 2 a [\cos(x) + \frac{a}{4}\cos(2x)] $$

So for a square-law transfer function, we will only see second harmonic distortion, and the level of that distortion will be directly proportional to the input signal level: $a / 4$.

If we compare the distortion level plot with the bipolar transistor distortion level plot, they are almost identical, with the 3rd harmonic and above missing.

Vacuum Tubes

Vacuum tubes work a little differently. There is a 3/2 power relationship between the output plate current and a combination of the plate-to-cathode and grid-to-cathode voltages. There has traditionally been modeled, based on the physics, as:

$$\begin{eqnarray} i_P &=& K(\mu v_{GK} + v_{PK})^{3/2} &\text{, for}& (\mu v_{GK} + v_{PK}) \ge 0 \\ &=& 0 &\text{, for}& (\mu v_{GK} + v_{PK}) \lt 0 \end{eqnarray}$$

Where:

$i_P$ is the plate current in Amperes, $K$ is a device parameter ($1.73 \times 10^{-6} $ for a 12AX7), $\mu$ is the tube's amplification factor (83.5 for a 12AX7), $v_{GK}$ is the grid to cathode voltage, and $v_{PK}$ is the plate to cathode voltage.

[References Smith, Leach, Spangenberg.]

Those curves look like this, for 12AX7 values. I'm using the 12AX7 as an example throughout because it is probably the most popular tube on the planet.

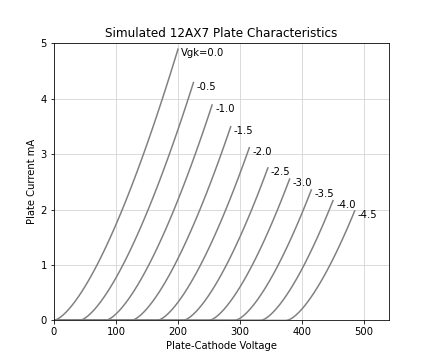
And we can compare that set of curves to the ones on the 12AX7 data sheet.

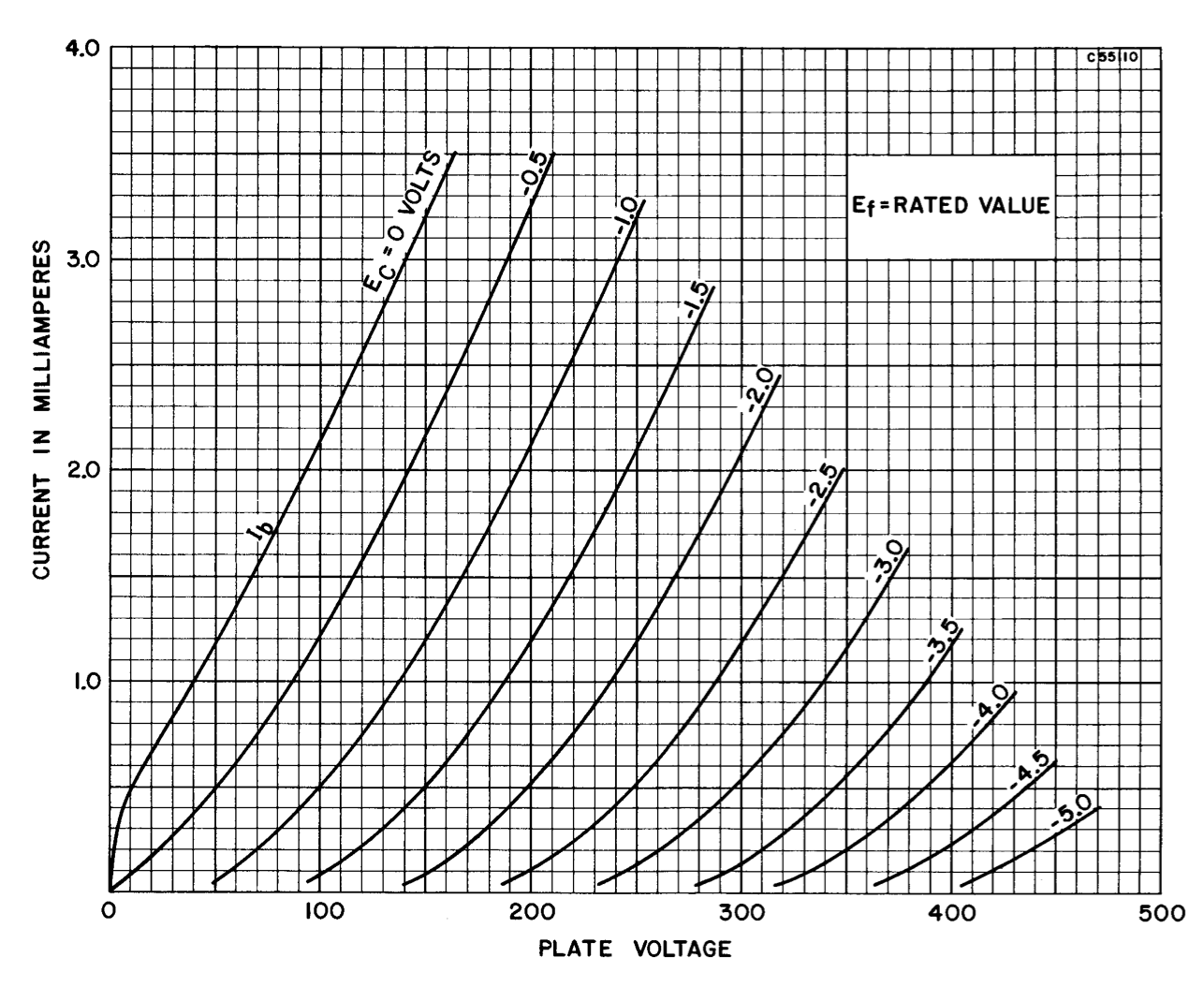
It is traditional to limit the top-right of the curves by the rated power dissipation of the tube, in this case 1 Watt.

In normal operation the grid voltage is below the cathode voltage. If the grid does go more positive, it will start drawing substantial current.

This equation is based on vacuum tube physics, and is used as the basis for many Spice models, such as the Leach model. The equations for tetrode and pentode tubes are similar. There are also more complex equations available that incorporate measurements of the characteristics specific tube model numbers. For this discussion we will stick to this 3/2 power equation.

First there seems to be a little confusion; the folklore assured me that vacuum tubes were square law devices, and the physics shows a 3/2 law function. What does a 3/2 law function even look like, and what is the harmonic structure like? Here is the triptych for a 3/2 power curve running at 10% distortion:

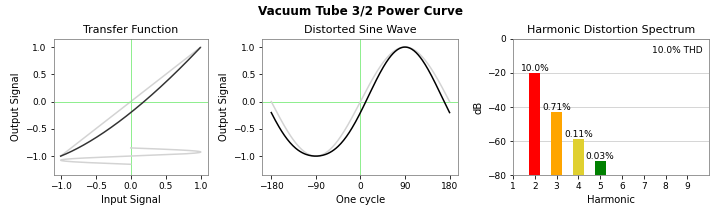
The 3/2 power curve is similar to the square law curve, the shape of the curve is slightly different, and it contains predominantly 2nd harmonic distortion, with 3rd, 4th, and 5th harmonics present at descending levels, although not dropping as rapidly as the exponential curve.

However... those curves above are nothing like the horizontal lines you would see with a current source. These are diagonal lines similar to a resistor, because the plate current depends on both the grid voltage and the plate voltage in the above equation. So unless there's some unusual "cascode" topology holding the plate voltage constant, we have to consider the output plate voltage, which means we need a supply voltage and a plate load resistor. For a typical 12AX7 preamp stage, that would be about 400V and about 100K ohms.

$$v_{PK} = V_{B+} - R_P \ i_P $$

Where:

$v_{B+}$ is the supply voltage, and $R_P $ is the plate resistor.

Which provides an output voltage of:

$$\begin{eqnarray} v_{PK} &=& V_{B+} - R_p K(\mu v_{GK} + v_{PK})^{3/2} &\text{, for}& (\mu v_{GK} + v_{PK}) \ge 0 \\ &=& V_{B+} &\text{, for}& (\mu v_{GK} + v_{PK}) \lt 0 \end{eqnarray}$$

As the $v_{PK}$ is on both sides of the equation, it is not solvable algrebraically; we can't write an output function of just the input.

A graphical solution superimposes a "load line" over the above curves. A line is drawn relating the current through plate resistor to the voltage at the plate. If the tube is biased off and not conducting there will be no current through the plate resistor and the output voltage will be the full $V_{B+}$ value. If the vacuum tube is shorted, the current through the place resistor will be $V_{P} / R_P$ and the output voltage will be 0. It's easy to plot these extreme points and draw a line between them. And the output voltage will be the intersection of the tube curve with that line, effectively solving the equations simultaeneously.

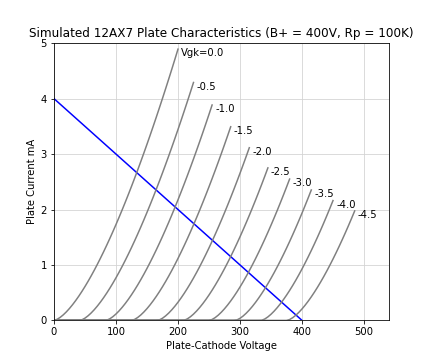
So a change of 1 V on the grid gives us a change of 50 V on the plate, for a gain of 50.

We can also solve the equation numerically. Here is a plot of the output voltage to input voltage for the circuit:

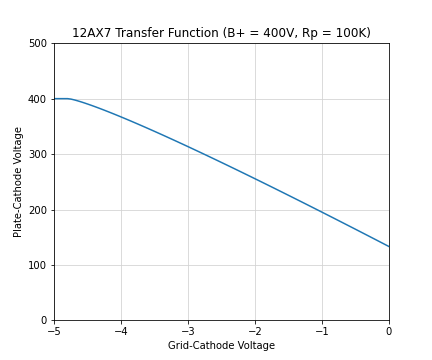
So that looks quite linear, but not completely. It certainly seems more linear than a 3/2 power curve or a square law curve.

Here is the distortion triptych for that circuit.

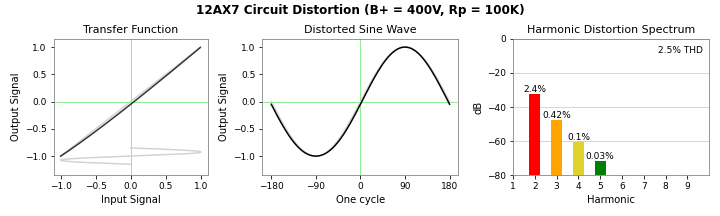
The vacuum tube equation, above, can be interpreted as negative feedback around a 3/2 power nonlieaerity.

A small amount of negative feedback has several effects; it linearizes the curve, reduces the gain, and reduces the signal level before the nonlinearity, which further linearizes the curve. But it can also be driven with a higher level input signal, and would have to be in order to maintain a given output.

The amount of feedback is defined as the ratio of open-loop gain to closed-loop gain. So in this particular situation the $V_{PK}$ factor in the equation essentially adds 12dB of feedback.

I originally presented the triptych curves with a 10% total harmonic distortion, which is larger than what would be acceptable performance, to clearly present the difference in curves. I can't do that here with the 12AX7 circuit, I couldn't get more than 4% harmonic distortion without clipping, and we know that the clipping isn't being modeled accurately in the equation, so that would be misleading. I had to back off the input level a little bit for these curves. So in practice, vacuum tubes have very low distortion.

And for completeness, here is that 12AX7 circuit distortion with respect to signal level:

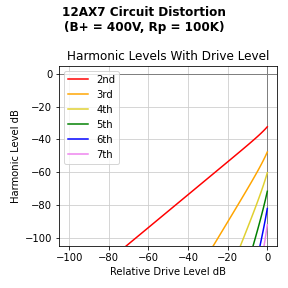
This finding is consistent with Marshall Leach's finding, "It can be seen that the second harmonic distortion is almost equal to the total harmonic distortion for each case. This indicates that the principal distortion created by the amplifier is second order."

Though Leach continues, "It has been postulated by many that this could be the principal reason for the difference in the sound of vacuum-tube and solid-state amplifiers.", which is where I disagree.

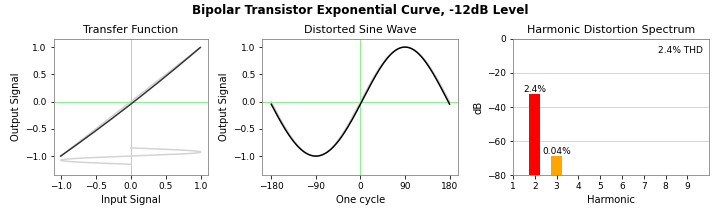
And if we take the 10% distortion bipolar transistor curve above and reduce the input signal level so that the total harmonic distortion is the same as the vacuum tube curve, 2.4%, we can see that the bipolar transistor curve has negligeable harmonic content above the 2nd.

-12dB bipolar transistor exponential triptych

Conclusion

In normal operating voltage gain circuits, the three types of devices, bipolar transistors, field-effect transistors, and vacuum tubes, all have very similar nonlinearities. They can all be described as a slight arc. And the harmonic distortion resulting from that arc is, at least, 90% second harmonic. And the presence of other harmonics would be dependant on circuit details and device parameters.

And in typical voltage gain configurations, both bipolar and FET transistors seem to have less harmonic content above the second harmonic than vacuum tubes.

And the bipolar transistor configured as a current gain stage is completely linear, at least as far as modeling goes.

And these findings run pretty much opposite the audio folklore.

References

The Jupyter Notebook code for this article is available here: https://github.com/dontillman/distortion-article .

W. Marshall Leach, SPICE Models for Vacuum Tube Amplifiers , 1995

Ralph J. Smith, Circuits Devices and Systems, 1976

K. R. Spangenberg, Fundamentals of Electron Devices, McGraw-Hill, 1957

Sylvania Electric, 12AX7 Data Sheet , 1955

J. Donald Tillman, Harmonic Distortion, Odd- and Even-Order , 2022