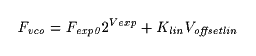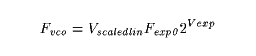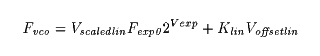This is the first of a set of articles about a new Voltage Controlled Oscillator (VCO) design for electronic music applications based on a Quadrature Trapezoid wave oscillator core.  Here I want to discuss the basic design, its goals, and applications.

The VCO core is the heart of the oscillator; the part of the circuit responsible for determining the frequency of oscillation as well as the basic capabilities of the unit.  The VCO core is supplemented with input circuitry to interface with the input control voltages and output circuitry to provide a number of desired waveforms.  So while electronic music VCO's produce many waveforms, they are almost always implemented as a sawtooth or triangle wave VCO core with a set of waveshaping circuits to provide the remaining waveforms.

What is a Quadrature Trapezoid?  It's a pair of trapezoid-shaped waveforms; one is called the Trapezoid Sine and one is called the Trapezoid Cosine.  They're 90 degrees apart so that the horizontal section of one wave corresponds to the the sloping section of the other.  This is what they look like:

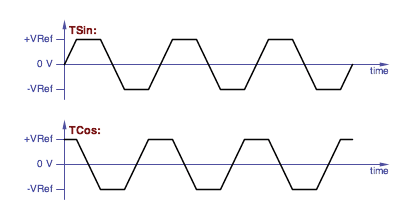
Trapezoid sine and trapezoid cosine waveforms.

(I made up the terms Quadrature Trapezoid, Trapezoid Sine and Trapezoid Cosine.  I also abbreviate Trapezoid Sine as TSin and Trapezoid Cosine as TCos.)

I offer the quadrature trapezoid VCO core as an alternative to traditional VCO cores for both the audio and low frequency (control and modulation) ranges.

The quadrature trapezoid VCO has a number of interesting features:

• Quadrature outputs
• Graceful thru-zero FM capability
• Exponential, Scaled Linear, and Offset Linear voltage control
• Audio or low frequency range
• Classic waveforms are easiliy derived from the quadrature trapezoid waves
• Phase-correct classic audio and LFO waveforms available
• Multicycle voltage controlled phase shift is possible

(I'll be defining what some of those strange phrases mean later in this article.)

One of the goals of this project is to create a break with tradition and provide an alternative VCO design with new features and new modes of operation.  The VCO is the primary source for sounds and modulation sources in electronic music synthesizers, yet it is often said that the filter is the heart of a synthesizer.  This is because there are more available variations in filter designs and each filter design has side effects that create an interesting sonic character.  I'll claim that this situation is because VCO designs are too much alike, have been stuck in a rut for a few decades and need to jump in a new direction to be more imaginative and musically useful.  So exploring new territory is important.

The original incentive of this project was the challange of building a VCO that could perform thru-zero Frequency Modulation (FM) -- this is where a control voltage can tune the oscillator down through 0 Hz to negative frequencies in a graceful manner.  This is a major component of FM synthesis.  While easy to implement in the digital world, it is a really difficult problem in the analog domain. 

Exactly why would anyone want to tune an oscillator to negative frequencies?

• FM synthesis
• Chorus effect by FM modulating an LFO with an audio signal
• Rotating speaker and rotational sound source effects
• LFO modulation in general
• Local oscillator for a Bode/Moog style frequency shifter
• Chaotic systems
• Analog computer simulation of rotating objects

Implementing analog thru-zero FM that performs gracefully near 0 Hz is especially difficult.  I'd like to be able to run the VCO near 0 Hz and modulate it both positively and negatively from there, and be able to do so without any glitches.  I couldn't find a way to do this with traditional VCO cores.

In the digital domain:

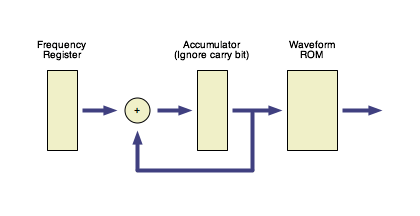
A block diagram of a basic digitally controlled oscillator (DCO) implmemenation.

The standard digital implementation of a VCO incorporates a register containing the frequency value, an accumulator, and a lookup table.  On each clock pulse the value in the frequency register is added to the accumulator, the carry bit is thrown away, and the accumulator value maps to a waveform value with a waveform lookup ROM.  The digital VCO is easily tuned to negative frequencies by setting the frequency register to a negative (two's complement) number.

(Now back to analog...)

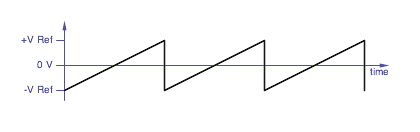
The classic sawtooth waveform.

In an analog sawtooth VCO core, the input control voltage is converted into a current source that charges the capacitor linearly up to a reference voltage point, at which the capacitor is quickly discharged.

Taking the sawtooth VCO core to negative frequencies requires ramping in the opposite direction, sensing a negative reference voltage and also resetting the capacitor voltage in the other direction.  But after the reverse reset the waveform is at a point where it's ready to be forward reset again.  It's very easy for the wave to get stuck at one state or oscillate inappropriately between the two resets.

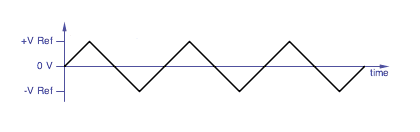
The classic triangle waveform.

The triangle wave VCO core is a better candidate for thru-zero operation because there are no sudden discontinuities.  The input control voltage is (effectively) converted into positive and negative current sources, the positive current source charges the capacitor linearly up to a positive reference voltage, at that point the VCO switches state and the negative current source discharges the capacitor linearly down to a negative reference voltage where the VCO switches state back.

But it turns out to be very difficult to take a triangle VCO core through to negative frequencies.  For one thing, the positive and negative reference voltages could be approached from either the forward or reverse directions.  Hitting the postive reference voltage no longer implies that we are going forward or that inverting the current source will switch direction.

If the control voltage goes through zero at the same time the triangle wave hits a reference voltage then it shouldn't be necessary to switch current sources at all.  If the wrong decision is made when the triangle wave hits a reference voltage, the triangle voltage could get lost beyond the reference voltage.

What exactly defines the states?  What exactly defines the transitions between the states?  What about the case where we go to a state boundry and bounce back without actually changing states?  Does the state depend on knowing the polarity of the input control voltage?  If so, how is that affected by real world offset voltages in either the control circuitry or the capacitor voltages?

I could not find a way to address these issues with a triangle VCO core.

The fundamental problem is that voltage is a one dimensional quantity, while waves are continuous and cyclic; they need two dimensions to physically describe their state accurately.

The digital VCO addresses the two dimensions with a one dimensional accumulator value that automatically wraps around as a result of throwing away the carry bit.  There's a discontinuity at the wrap, but there's also a discontinuity on each clock pulse.

The state of a sawtooth core is described by a continuous voltage plus a momentary reset state.  The oscillator is effectively "off line" during the reset and comes back when the reset is finished.

The triangle core uses a continuous voltage plus a binary direction for it's two dimensions.  But the points where the binary part changes state are less clearly defined as the frequency nears 0 Hz.

I decided that I needed two continuous values for my two dimensions.  A sine wave and a cosine wave are an obvious approach, but maintaining the mathematical relationship between them near 0 Hz is difficult.  And it's difficult to derive other waveforms from a quadrature pair of sines.

The quadrature trapezoid core has two continuous values for its two dimensions, like a sine/cosine relationship.  And the quadrature trapezoid is easy to implement -- at any given time one of those values is changing while the other stays constant.

Instead of the traditional single ramping capacitor found in a sawtooth or triangle VCO core, the quadrature trapezoid VCO core uses two separate ramping capacitors.  The waveform is divided up into four quadrants.  During each quadrant one capacitor is ramping between a postive reference voltage ("+VRef") and a negative reference voltage ("-VRef") while the other capacitor is being held at one of those reference voltages.

Here is a plot showing the quadrature trapezoid waveforms and states:

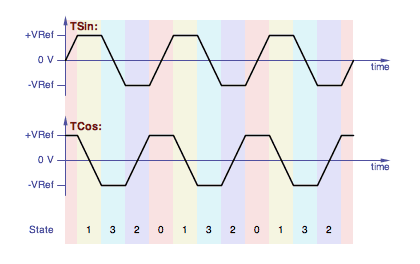
Showing the quadrature trapezoid states.

The order of the states is Gray Code, a binary counting system where only one bit changes at a time.  Here we go from binary 00 to 01 to 11 to 10 and back around to 00.  Or in reverse.

The state chages when the capacitor that's ramping crosses the positive or negative value of the capacitor that's being held at a reference voltage.

Here is the state diagram (the colors match the plot above):

State 0 TSin ramps forward TCos holds positive (TCos < TSin) (TSin < TCos) State 1 TSin holds positive TCos ramps backward (TSin < -TCos) (-TCos < TSin) (TSin < -TCos) (-TCos < TSin) State 2 TSin holds negative TCos ramps forward (TCos < TSin) (TSin < TCos) State 3 TSin ramps backward TCos holds negative State diagram showing the transitions between the four states.

Here the states are all well defined, the transitions between the states are well defined, and there are no discontinuities when transitioning between states.  Any offset voltages will only have the effect of altering the specific point where a transition between adjoining states occurs.

When the states are defined this way, it's very easy to derrive StateA and StateB, the first and second bits of the state value, by simply comparing the two capacitor voltages:

StateA is true when TCos < TSin
StateB is true when -TSin < TCos

That's illustrated in this drawing:

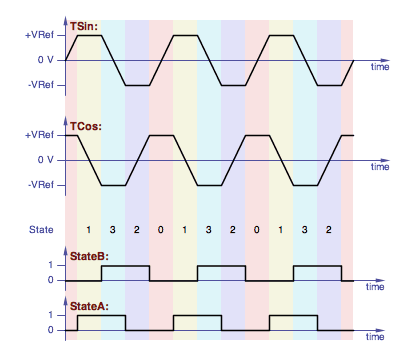
Quadrature trapezoid states with the state waveforms.

Here is a block diagram of the quadrature trapezoid VCO core implementation:

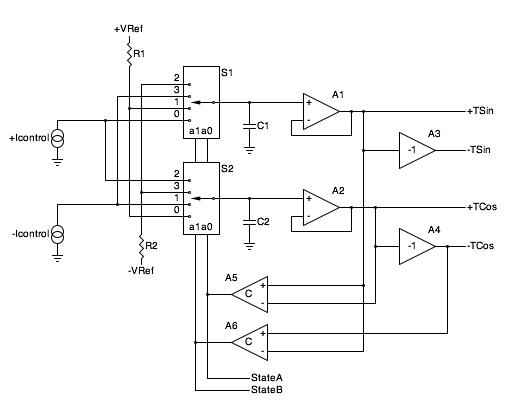
Block diagram of the quadrature trapezoid VCO core.

(The second article in this series presents a complete schematic.)

The VCO uses complementary current sources +Icontrol and -Icontrol to ramp the voltages on capacitors C1 and C2.  Each current source is capable of both positive and negative current flow (sourcing and sinking) and both are controlled by the input control voltages.  The current sources run "push-pull", so the current of one is equal and opposite the current of the other.

S1 and S2 are two halves of a dual 4-input analog multiplexer chip.  The multiplexors choose the source for both capacitors for each quadrant as follows:

State to C1 to C2 0 +Icontrol +VRef 1 +VRef -Icontrol 3 -Icontrol -VRef 2 -VRef +Icontrol The dual 4-input analog muliplexer steers four sources into two capacitors.

+VRef and -VRef are the reference voltages, typically +5.0 V and -5.0 V respectively.  The reference voltages define the amplitude of the trapezoid waveforms.

Voltage followers A1 and A2 buffer the capacitor voltage providing TSin and TCos outputs.  Amplifiers A3 and A4 each have a gain of -1 and provide the -TSin and -TCos outputs.

A5 and A6 are comparators.  These provide the StateA and StateB signals, defining which quadrant we're in, and those feed the analog multiplexer.

StateA and StateB are also available as separate outputs for other purposes (free square waves, waveshaping, voltage controlled phase shift, etc.).

A trapezoid is probably not the most useful musical waveform there is.  It doesn't have a lot of harmonic content and the harmonic content it does have contains only odd harmonics.  The waveform also cannot be morphed under voltage control (compared to a square wave which can have its duty cycle controlled).

However, the quadrature trapezoid is relatively easy to shape into the classic synthesizer waveforms.  And having quadrature phases available allows waveform conversion techniques that minimize glitches.

The triangle wave is easiest; simply average the TSin and TCos waveforms:

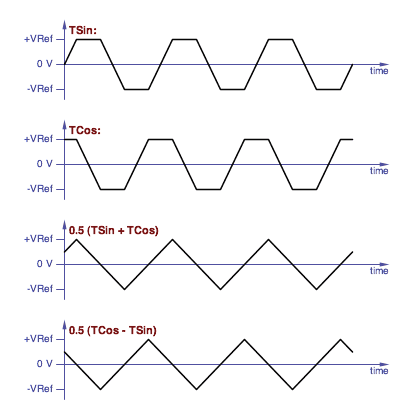
Averaging two quadrature trapezoid waves gives you quadrature triangle waves.

A second triangle wave in quadrature with the first is readily available by choosing the -TSin wave instead of the TSin.  And the triangles can be converted to sine waves with the classic triangle to sine shaper circuit.

It's only slightly more difficult to build a sawtooth wave from a quadrature trapezoid core.  One way is to use the StateB line to switch between two triangle waves:

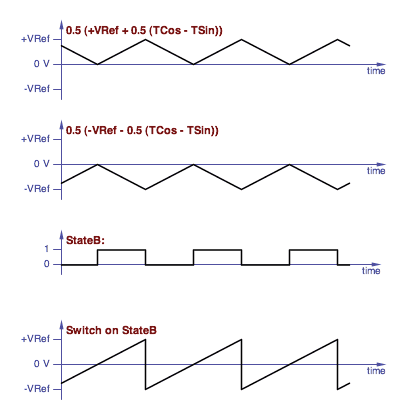
Constructing a sawtooth wave by switching between two triangles.

Another feature of the quadrature trapezoid core is that, since quadrature phases are available, it is possible to have much greater control over the phase of the generated waveforms.  Phase-correct waveforms are sets of waveforms that are crafted so that their relative phases are aligned for a particular purpose, and will be the subject of a later article.

It turns out that the core of a VCO is actually a current controlled oscillator, because it is a current source that ramps the capacitor voltage.  So the input to a VCO needs to be converted to a current.  And with a thru-zero VCO, that current needs to be able to swing both positive and negative.

Typically VCO's for musical work are exponential; their frequency is an exponential function of the input control voltage.  This is the way we hear; the frequencies of an equal tempered scale are exponential, and the ratio of one note to the next chromatic note is a constant.  To be especially useful, the input control voltage is typically calibrated to 1.0 Volt/Octave, so increasing the input control voltage by 1.0 V doubles the frequency and decreasing the input control voltage by 1.0 V halves the frequency.

An exponential control voltage by itself cannot tune a VCO to negative frequencies; as the control voltage goes more negative the frequency goes toward zero.  Thru-zero FM requires linear frequency control.

When you have both exponential and linear control, there are two ways the linear control can be implemented; offset linear and scaled linear.  (I made up those terms also.)

In the offset linear case, the linear control is added after the exponentional control:

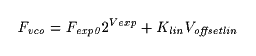
Where:
F_vco is the frequency of the VCO in Hertz
F_exp0 is the frequency in Hertz with a 0 V exponential control voltage
V_exp is the exponential control voltage in Volts
K_lin is the linear scaling constant, in Hz/Volts
V_offsetlin is the offset linear control voltage, in Volts

A typical application of offset linear control would be to detune an oscillator by a fixed amount for a chorus effect.  This would involve a very low value K_lin constant and the oscillator would only go to negative frequencies at low values of V_exp.

In the scaled linear case, the linear control is effectly placed before the exponential control and therefore scaled or multiplied by it:

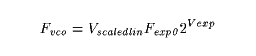
Where:
V_scaledlin is the scaled linear control voltage in Volts

V_scaledlin might be nominally held at 1.0 V, raised to 2.0 V to double the frequency of the VCO, or lowered to -1.0 V to bring it down to the mirror-image negative frequency.  This arrangement is much more useful for FM Synthesis.

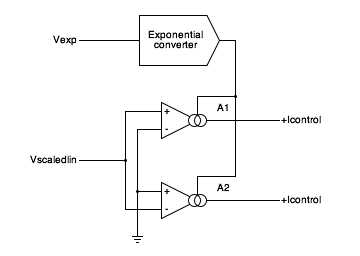
Here is a block diagram of the circuit I use to generate +Icontrol and -Icontrol:

Block diagram of the circuit to generate the control currents from an exponential control voltage and a scaled linear control voltage.

A1 and A2 are Operational Transconductance Amplifiers (OTA's).  An OTA is an opamp-like device whose output is a current source with a current propotianal to the differential input voltage.  The OTA gain is a transconductance, and is proportional to the bias input current.  An exponential control voltage input, Vexp, drives an exponential converter which provides the bias currents for the two OTAs.

Of course you can have both scaled linear and offset linear inputs:

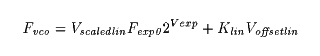
And of course this would lead to a discussion about the most appropriate value of K_lin, which would lead to making it voltage controlled over a wide range.  Which is effectively the same as a pair of scaled linear controls in parallel.  And it is completely practical to parallel multiples of the above circuit.

The quadrature trapezoid core also enables the implementation of voltage controlled phase shift over a multiple cycle range.  I'll cover the details of this in a later article.

While the Yamaha DX7 synthesizer is well known for its use of FM Synthesis, it really works with phase modulation. (The phrase FM Synthesis is used as a generic term to describe both frequency and phase modulation.)  So analog versions of many DX-7 algorithms are good applications for voltage controlled phase shift.

This article is an introduction to the quadrature trapezoid VCO describing the basic operations and features and suggesting some possibilities.  Future articles will explore this more.

ASM-1 Analog Synthesizer Module,
Gene Stop and Magnus Danielson.

Moog Modular System Technical Service Manual,
Norlin Music.

ARP 2600 Service Manual,
ARP Instruments, Inc., September 1977.

The Synthesis of Complex Audio Spectra by Means of Frequency Modulation,
John M. Chowning, Journal of the Audio Engineering Society, 1973.

US Patent 4,018,121: Method of Synthesizing a Musical Sound,
John M. Chowning, Issued April 19, 1977

US Patent 4,554,857: Electronic Musical Instrument Capable of Varying a Tone Synthesis Operation Algorithm,
Tetsuo Nishimoto, November 26, 1985

Bucha 258B Oscillator Module Schematic,
Don Buchla, June 1970.

CA3280 Dual Operational Transconductance Amplifier,
Intersil data sheet.

19 July 2003  Originally published.
24 July 2003  Spelling, typos, tweaks.