I'm sure you've heard of Moore's Law. It is not an actual law, but rather Gordon Moore's observation that the complexity of integrated circuits can double every two years. The predictive accuracy has been so good for so long that it has been dubbed a law. But regardless of the title, such a sustained level of exponential growth is remarkable.
How is Moore's Law possible? What is the mechanism behind it? I haven't seen it mentioned in the literature. Is it applicable to other fields? The Wikipedia page doesn't help.
I've been working intimately with integrated circuits since about 1970, and I'd like to present some thoughts on the topic. I think it's really interesting.
Gordon Moore was one of eight founders of Fairchild Semiconductor in Palo Alto, California, in 1957. Fairchild invented the planar process, which allowed transistors to be manufactured more efficiently and at significantly lower cost than before. And the process was adaptable to making integrated circuits. Fairchild totally pioneered the field, and by 1965 the Fairchild catalog included an impressive set of product lines of diodes, transistors, and digital and linear integrated circuits.
Also in 1965, Gordon Moore published, "Cramming More Components onto Integrated Circuits". Besides most likely being the first electrical engineering paper to include the word cramming in the title, it included this quote:
"The complexity for minimum component costs has increased at a rate of roughly a factor of two per year (see graph). Certainly over the short term this rate can be expected to continue, if not to increase. Over the longer term, the rate of increase is a bit more uncertain, although there is no reason to believe it will not remain nearly constant for at least ten years. That means by 1975, the number of components per integrated circuit for minimum cost will be 65,000."
The phrase "minimum component costs" describes an integrated circuit that pushes the boundries of the number of transistors while at the same time providing an economic benefit suitable to the marketplace. So this would exclude any expensive heroic laboratory efforts.
The Y axis on that chart is log base 2, so it should be read as 1, 2, 4, 8,... to 65,536.
And sure enough, Fairchild had gone from their first simple IC introduced in 1961 with 4 transistors, to the most complex in their 1965 catalog at 19 transistors. And the 1966 Motorola Semiconductor catalog has an IC with 45 components.
Doubling every year is a crazy fast rate; a factor of 1024 every decade. While that was the apparent slope during the initial period of integrated circuit development, it wasn't realistic. So ten years later, in 1975, Moore adjusted the rate in a speech called "Progress In Digital Integrated Electronics":
"[...] the rate of increase of complexity can be expected to change slope in the next few years as shown in Figure 5. The new slope might approximate a doubling every two years, rather than every year, by the end of the decade. Even at this reduced slope, integrated structures containing several million components can be expected within ten years. These new devices will continue to reduce the cost of electronic functions and extend the utility of digital electronics more broadly throughout society."
And from there it kept going, at roughly the same rate:
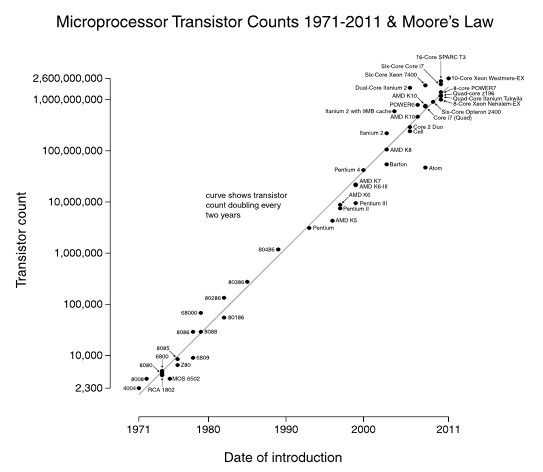
Doubling every two years is an example of exponential growth. Exponential curves are of the form:
where a is positive. They look like this:
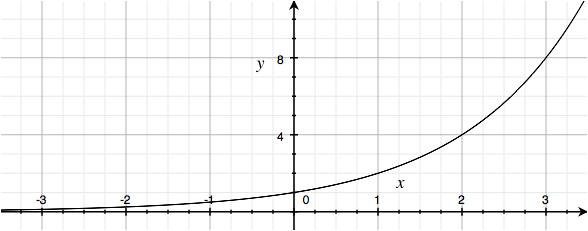
Figure 2. Plot of .
The Y value grows proportionally each step along the X axis. The curve tilts up, the slope of the curve increases, and the slope of the curve keeps increasing.
Changing the base of the exponentiation, or scaling the x-axis or y-axis, or shifting along the x-axis or y-axis; these are all equivalent and don't have an effect on the shape of the curve. A sequence like [1, 2, 4, 8] is the same shape as [1024, 2048, 4096, 8192].
It's easy to find processes with exponential curves over the short term, just as it is easy to find processes with just about any curve over the short term. Processes that maintain an exponential curve over the long term are more interesting. That doesn't just happen; there has to be a particular type of mechanism behind it.
This is the generalized equation for exponential growth:
Where is the exponential rate of growth, is the time, and is the value of the exponential processes, normalized to 1.0 at time , the reference time.
Mathematically, the derivative, or slope, of an exponential curve turns out to be proportional to the value of curve itself at any given point.
And thus:
One of the interesting things about exponential curves is that they serve as a fingerprint, forensic evidence of a very specific kind of mechanism: positive feedback. So when you see an exponential curve the cause is very likely going to be some sort of positive feedback. It is very difficult to name an exponentially growing process that operates without involving positive feedback.
I'm not using the popular definition of "positive feedback" or "negative feedback", as a compliment or a complaint. I'm using the technical definition, which involves a process that performs some function, sampling some of the result of that process and either reinforcing (positive feedback) or countering (negative feedback) any changes.
Negative Feedback
Negative feedback performs a correcting function. An example would be the thermostat in your home; when the measured temperature falls below a certain value the thermostat cranks up the furnace, and when the measured temperature has risen above that value the thermostat turns the furnace backs off. So the thermostat makes an adjustment in the opposite direction.
Our bodies naturally employ negative feedback so much to move around that we don't even think about it. Just walking down the street, we're always correcting for road conditions, or slope, or wind. You would never want to drive or take a walk blindfolded, memorizing the path, and unable to make corrections as you go.
It turns out that any stable system in practice requires a negative feedback mechanism to adjust to survive. Negative feedback compensates for errors, for drifts, for the effects of external forces, and so forth.
Positive Feedback
Positive Feedback does the opposite; for any change, positive feedback reinforces that change.
Compound interest would be an example, quite literally, as a percentage of the value of the account is summed back in. The process then repeats, just scaled up a little bit, for exponential growth.
And viral cat videos. When sharing a video with someone has a tendency to cause that person to share it with someone else, that's an example of positive feedback.
Long term exponential growth also applies to business plans. If you want a business to do well over the long haul, it should have a roughly constant rate of growth, and thus an exponential curve fueled by the positive feedback of a good business model.
So stability is the fingerprint of negative feedback, and exponential growth is the fingerprint of positive feedback.
Let's say I have a semiconductor factory right here. And let's say I invest in some good engineering research and development, and as a result I am able to manufacture and offer for sale a new inproved chip that is more complex, or performs better, or does more. Great!
My customers can use this new chip to make better products.
One customer happens to be in the photolithography machine business. So now, they can make better photolithography machines. It turns out that I use photolithography machines on my manufacturing floor to make chips. So with these new machines I can improve my manufacturing process and I can then make... even better chips.
Semiconductor Manufacturer
That is a positive feedback loop. But there's more...
Another one of my customers makes test equipment. And they can use my new chip to make better test equipment. And you know that I use all sorts of test equipment to run quality assurance testing on my chips and to characterize and improve my manufacturing processes. So I can then install that new test equipment in my factory and make... even better chips.
Semiconductor Manufacturer
It keeps going. Better chips for better computers to design and simulate better chips.
So there are a number of positive feedback paths working in parallel. Heck, even products that my competitors make can improve my products. (!!!) What an amazing system.
It even works indirectly: I can make a better chip, that chip is used in a machine my competitor uses to make his own better chips, and those chips are used by another company to make better wafer handling machines that I use on my factory floor.
And that is the basic mechanism behind Moore's Law; any improvement to the product has a side effect of improving the manufacturing of the product. And it operates in a powerful postive feedback loop.
Note that this mechanism has more in common with economics and systems theory than semiconductors or electronics. If you look around you'll see positive and negative feedback loops all over the place, along with their consequences.
Exponential growth for a short period of time is somewhat common. Heck, an appropriately shaped bit of noise can appear exponential over a sufficiently short period of time. But exponential growth over the long term is a rare occurance.
Physical things usually have physical limits, so the most likely limit is that the main process can only reach a value so high. How does the semiconductor industry get around that?
For the main process, semiconductor manufacturing has actually hit dozens of physical limitations over the years, and every time there has been enormous economic incentives to alter the process, work around it, or to come up with a replacement technology. Early RTL logic was replaced by DTL logic, then TTL logic, and TTL logic with Schottky transistors for speed, then MOSFET transistors for density, then complementary MOSFET designs for power consumption, then lower power supply voltages, and so on. These are all specfic variations of implementation technologies.
After those physical limits are approached, there are new opportunities for architectural variations. In present day we are hitting a physical limit on clock speed, and so now we are seeing processors with multiple cores. And separate processors optimized for graphics operations. And neural networks.
And as the limits of silicon, itself, are approached, there may be new opportuities in light-based or quantum computing.
If the feedback loop is physical, it too might have a physical limitation, and a limit to the amount of feedback would limit the rate of growth. Often the feedback loop might not be able to stay in place, or might not be applicable for one reason or another, as the growth changes the landscape.
The feedback paths in semiconductor manufacturing also have physical limits, but these limits keep rising alongside the product improvements. After my new chips come out with improved performance, I'm going to need more powerful test equipment for the next improvement. This places a new demand on the test equipment manufacturers. In the semiconductor industry, this feedback path appears to have no limits.
The semiconductor industry, has significant redundancy with multiple feedback paths operating in parallel. If a number of those feedback paths poop out for whatever reasons, the rest will chug along just fine.
So far the discussion has been about the supply side. Demand is also import; without demand there is no economic need for the supply. So the mechanics of Moore's Law also requires a roughly continuously increasing demand for higher density integrated circuits.
And historically, we see that has been the case. The earliest chips contained a very small number of logic gates (2, 3, or 4). And there was a demand for larger building blocks such as registers and adders. Then even larger building blocks. Then subsystems on a chip, microprocessors and so on. Each improvement opens up new products and new applications.
And software development, as an industry, has put more and more demands on hardware.
In his book, The Singularity, Ray Kurzweil extrapolates the basic mechanism of Moore's Law to a time before integrated circuits, including transistors, vacuum tubes, electromechanical, and straight mechanical computing systems.
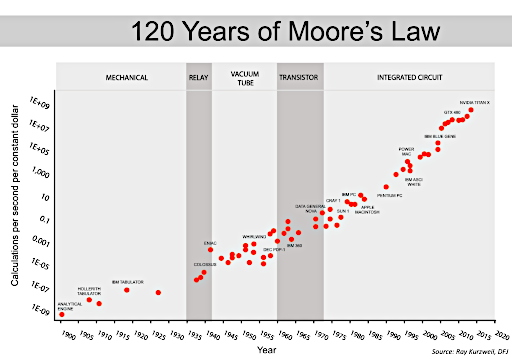
The curves don't really change. The mechanism behind Moore's Law is not specific to silicon.
So the engine of Moore's is where advancing a technology has a consequence of accerating the next advance. Kurzweil applies this to software development and machine learning, leading to The Singularity.
Every past prediction about the limitations of Moore's Law has proven wrong. And many bad engineering decisions have been made by not taking Moore's Law into account.
So I'll just propose that Moore's Law will continue for roughly as long as the positive feedback and demand mechanisms I've described here are still in effect.
Gordon E. Moore, "Cramming More Components onto Integrated Circuits" , , Electronics Magazine, April 19, 1965
Intel, A Conversation with Gordon Moore: Moore’s Law
Gordon E. Moore, "Progress In Digital Integrated Electronics" 1975 IEEE Speech
Wired Magazine, How Gordon Moore made Moore's Law
Fairchild Semiconductor, 1965 Semiconductor Catalog at Archive.org
Motorola Semiconductor Products, Semiconductor Data Book, 2nd Edition, August 1966, at BitSavers
Computer History Museum, Fairchild Semiconductor: The 60th Anniversary of a Silicon Valley Legend
Computer History Museum, 1960: First Planar Integrated Circuit is Fabricated
John Walker, Fifty Years of Programming and Moore's Law
Wikipedia, Fairchild Semiconductor