A Palette of Static Audio Waveforms
Donald Tilllman, Oct 14, 2016
Introduction
The Voltage Controlled Oscillator (VCO) has always been the primary audio source for electronic music synthesizers, and has always supplied a small number of waveforms named with simple geometric shapes: sine, triangle, square, and sawtooth. These waveforms have not changed since the very first Moog oscillators.
It's often said that "the heart of a synthesizer is the filter". Is that because oscillators are uninteresting? Is it time to rethink things? Can we do better?
VCO Waveforms
Let's start with a quick review of the classic waveforms:
- Sine Wave
- 'Just the fundamental frequency, no harmonic content. So it's not directly applicable to subtractive synthesis.
- Square Wave
- The notable feature of a square wave is that it has only odd harmonics and a distinctly hollow character. It sounds a bit like a clarinet, which has mostly odd harmonics due to the physics of wave reflections in a cylinderical bore. The square wave has a lot of harmonic content, so it needs to be filtered down to be musically useful.
- Triangle Wave
- The same odd harmonics as the square wave, but the harmonics fall off in strength much faster for a much mellower sound.
- Sawtooth Wave
- A bright waveform with all harmonics. Bowed strings operate like sawtooth waves; the friction of the bow pulls on the string until the force overcomes the friction and the string snaps back.
(I am omitting the variable width pulse waveform only because the discussion is limited to fixed static waves.)
In practice, the musician scans down the list, skips the sine wave as it has no harmonics, skips the square wave as there is probably little interest in a hollow clarinet sound, skips the triangle wave as there is probably little interest in a mellow hollow clarinet sound, and usually settles on the sawtooth wave. And then turns their attention to the filter. 'Pretty much every time.
So most melodic synthesizer playing starts with the timbral nature of a bowed string with the occasional clarinet, and filtered. Of course that's a crass generalization, but the point is that we are stuck in a rut, especially considering that electronic music is supposed to open up possibilities.
The obvious response is more geometric waveform shapes. Perhaps pentagons? Or octagons? Almost all VCOs use a sawtooth oscillator core with the strategy of implementing nonlinear mapping functions to derive arbitrary waveform shapes from the core. But efforts at creating new geometric shapes have seen minimal returns, and generally deemed to not be worth the trouble. So even after about 50 years, the original set of four waveforms are still being used.
One might even be tempted to give up. Any static waveform is going to consist of nothing more than a fundamental with harmonics, and thanks to the sawtooth wave, we've already heard all the harmonics. So perhaps there's nothing left.
Let's take a closer look at the waveforms...
Harmonic Series
As a review, the sawtooth wave contains all harmonics, each at a strength of for the nth harmonic. So the harmonic series for the sawtooth is:
Where is the waveform voltage, is the radian frequency, is the frequency in Hz, and is the time in Seconds.
While the strength of each harmonic is dropping, the number of harmonics per octave doubles with each octave up. And there is some distracting math here involving power vs. voltage... but suffice it to say this is a lot of harmonic content.
Note that with this series the slopes of all the sine wave harmonics are positive at , the beginning of every sine cycle, and these slopes sum together, creating an instantaneous positive reset pulse, with the ramp sloping linearly down from there. So the polarity here is opposite from the way the classic sawtooth wave is drawn.
The square wave has a harmonic series similar to the sawtooth wave, but with just the odd harmonics:
And the triangle wave has the odd harmonics of the square wave, but the harmonics drop off with for the nth harmonic:
That's a steep attenutation; the dominant 3rd harmonic is down 19dB, and the higher harmonics much more so.
Also note that this harmonic series is aligned by cosines instead of sines.
(Minor technical note: There is an equivalent harmonic series written with sines, but cosines are clearer, especially as this article progresses. With the exception of the traditional waves at the top, the waveform graphics presented in this article have the fundamentals of all waveforms aligned with the sine wave, and the amplitude adjusted for a constant RMS voltage level.)
Waveform Shapes vs. Spectrums
This article concerns audio waveforms, waveforms that we listen to. But our sense of hearing cannot actually discern the shapes of waveforms, geometric or otherwise. Waveforms that are graphically similar can sound very different, and waveforms that sound nearly identical can be graphically very different. The phases of harmonics are usually inaudible, but their effects on the graphical shape of the waveform are substantial. (For an entertaining set of examples, see my article Square Wave Variations.)
Thus, for audio applications it makes sense to consider the spectral qualities instead of the graphical shapes of the waveforms. Conversely, if the topic were Low Frequency Oscillators (LFOs) as modulation sources, then the situation would be reversed, and we would be far more interested in the graphical shape than in the spectrum of the waveforms. But for audio, we hear spectrums.
Spectral Attributes
If we ignore the graphical shapes of waveforms, then what interesting spectral attributes should we consider? Two interesting attributes come to mind, attributes that have already been a part of this discussion: the strength of the harmonic content and the pattern of the harmonic content.
Square and sawtooth waves are examples of bright sounding waveforms with high amount of harmonic content, with the strength of the harmonics falling off at for the nth harmonic. And the triangle wave is an example of a mellow sounding waveform with a low amount of harmonic content, where the harmonic strength trails off at . So the first interesting attribute is the strength of the harmonic content, bright vs. mellow, or vs. .
And the sawtooth wave is an example of a waveform with all harmonics while the square wave has only odd harmonics. So a second interesting attribute is the harmonic pattern: spectrums with all harmonics, spectrums with only odd harmonics, and spectrums with only even harmonics.
These two attributes are orthoganal, they can exist in any combination. So we can set up a 2x3 array and place our current waveforms (minus the sine) into that array, like this:
| Mellow, Harmonics | Bright, Harmonics | |
|---|---|---|
| Odd Harmonics |
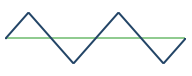
|
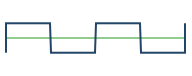
|
| Even Harmonics | ||
| All Harmonics |
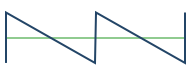
|
With this arrangement it seems pretty clear that there are three missing waveforms. And we can place those missing waveforms, not from their shapes, but from their implied harmonic content, and the shapes derived from there.
Here is the table with the new waveforms filled in:
| Mellow, Harmonics | Bright, Harmonics | |
|---|---|---|
| Odd Harmonics |

|

|
| Even Harmonics |
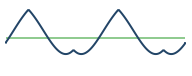
|

|
| All Harmonics |
|

|
Well, that's an interesting set of waveforms.
Let's Meet the New Neighbors
Center right is the eventooth wave. (This is a new waveform so I get to make up the name.)
The eventooth wave is bright, with strong harmonics, but even harmonics only. The harmonic series is:
One might think of an eventooth wave as a square wave but with the odd harmonics replaced with even harmonics. Or think of it as a sawtooth wave with the odd harmonics removed.
Center left is the evenangle wave. (I also made up this name.)
The evenangle wave is also even harmonics only, but mellow, with the harmonics trailing off at . The harmonic series is:
One might think of the evenangle wave as a triangle wave, but with the odd harmonics replaced with even harmonics. And like the triangle wave, the series is aligned by cosines.
Going from odd harmonics to even harmonics effectively moves each harmonic down the steep falloff rate, leaving the evenangle wave with slightly stronger harmonic content than the triangle wave.
And, finally, in the lower left is the parabolic wave, which is also mellow, with the harmonics trailing off at , and it includes all harmonics.
So the parabolic wave has the harmonic content of the triangle wave and eventangle wave combined. And the series is also aligned by cosines.
Demo
Now that we've seen what the new waveforms look like, let's listen and compare them to the standard waveforms. (This demo should work any modern browser.)
Instructions: Select one of the seven waveforms by name on the left. The selected waveform is displayed at the top, and the harmonic spectrum is displayed below.
The spectrum plot is log-log. The X axis is in octaves above the fundamental, so you can see the harmonics double in density with each octave up. The Y axis is the attenutation in dB. Note that -40dB is a voltage factor of 1/100th, or a power factor of 1/10,000th.
All three of the new waveforms include substantial 2nd harmonic content, and because of that, they will sound unusual, more vocal.
Integral / Derivative
There is an integral/derivative relationship between the corresponding mellow and bright waveforms. The triangle wave is the integral over time of the square wave, the evenangle wave is the integral over time of the eventooth wave, and the parabolic wave is the integral over time of the sawtooth wave. And vice versa for derivatives.
This relationship is also consistent with the harmonic series of the bright waveforms being sine-based while the harmonic series of the mellow waveforms are cosine-based.
Implications
It is interesting to present the mellow and bright waveforms side by side. The bright wavesforms have substantial harmonic content (or as Les Paul would say, "rip y'r ears off"), far more than is traditionally musical, and require a high-cut filter of some sort to tame them down, which is the very point of Subtractive Synthesis.
But the mellow waveforms do not need a filter; they are musically useful the way they stand. The steep falloff of harmonics is, effectively, their own filter. And we now have three flavors of mellow waveforms: odd, even, and all harmonics, each with their own characteristic sounds. And the new mellow waveforms have a little more harmonic content than the original triangle wave.
So one can imagine two different patching schemes with two different voices; a mellow wave without a filter and a bright wave with a filter. And a nice choice of waveforms for each.
Mixing Waveforms
Just listening to the raw waveforms, one might find the bright ones too bright and the mellow ones too mellow. As with a painter mixing the original colors on their palette, in practice one can mix the waveforms together for a remarkably diverse set of timbres.
When I play electric guitar, I often start out with a mellow jazz sound and mix in high end to taste. This palette of waveforms can work the same way; start with a choice of mellow waveforms and dial in a bright waveform to taste.
Waveform mixing is messy if the waveforms are not phase aligned, which can be tricky. This topic and other topics will be covered more in subsequent articles.
Conclusion
By ignoring shape and concentrating on spectral properties it is possible to develop a musically useful palette of audio oscillator waveforms covering a wide range of timbres in an easily navigible arrangement.