Exploring Walsh Functions
J. Donald Tillman
May 2020
(Sharing with colleagues. Please don't publish it on a mailing list or forum just yet.)
Back some time ago, the use of Walsh Functions was suggested for electronic music. What are Walsh Functions? They're sort of like a Fourier Series with square waves.
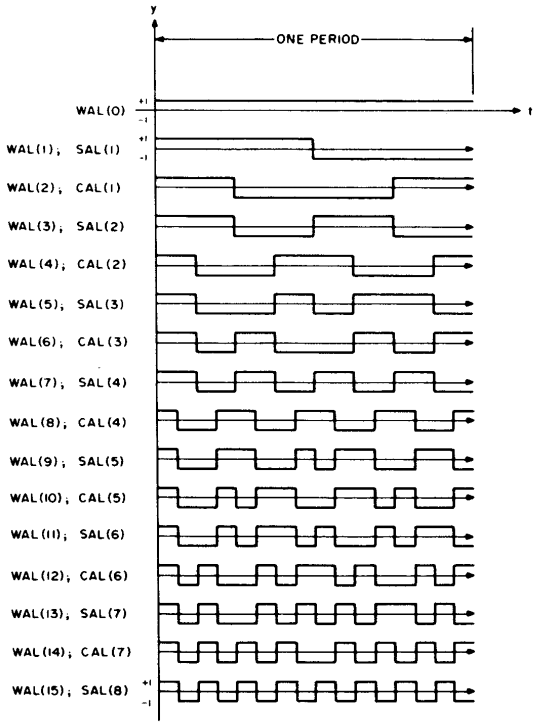
The illustration on the right is from Jacoby (references) and shows sine and cosine versions of the first 8 Walsh functions. (The nomenclature is a little weird; that's a side effect of the math.)
The writings at the time (Electronotes, etc.) were geared toward using Walsh Functions to digitally implement the classic oscillator waveforms. I don't believe such a thing was ever commercialized.
I'm not interested in digital approximations of perfectly working analog functions. But I am intrigued about the possibility of other musical applications of Walsh Functions. What is their timbre like? Can we apply them in a musically expressive way? They're certainly easy enough to generate.
Well, we have an opportunity to check them out. This is a software simulation of a potential oscillator that delivers a set of 8 Walsh functions, and lets you mix them down.
Instructions
These are the first 8 sine Walsh Functions. I've labeled them "W1" through "W8". ("SAL(1)" through "SAL(8)" in the above top diagram.) I tried the cosine versions also, but found no advantage to having both.
The sliders are "attenuverter" style, both positive and negative, with the zero at the center.
Click on the keyboard to play a note, or below to stop the note.
The Weighted Sliders button attenuates each slider by a factor of N. So the W8 is 1/8 the level of W1. I found it to be more intuitive this way. And you wouldn't want an 8x square wave to fry your tweeters.
The tones generated here are unfiltered and will be on the bright side. The intent is that these waveforms are going to be used in the context of classic Subtractive Synthesizer, like a square wave, and will got through a low pass filter. There is no filter in this demo.
Mapped Harmonics
Walsh Functions can be used to generate individual Fourier sine harmonics. And we can work those out from the Fourer Tranforms of the individual Walsh Functions, going backwards, solving a set of simultaneous equations. Those values are here:
| Harmonic | W1 | W2 | W3 | W4 | W5 | W6 | W7 | W8 |
|---|---|---|---|---|---|---|---|---|
| Fundamental: | 0.645 | 0.000 | -0.267 | 0.000 | -0.053 | 0.000 | -0.128 | 0.000 |
| 2nd: | 0.000 | 0.673 | 0.000 | 0.000 | 0.000 | -0.279 | 0.000 | 0.000 |
| 3rd: | 0.240 | 0.000 | 0.580 | 0.000 | -0.388 | 0.000 | 0.161 | 0.000 |
| 4th: | 0.000 | 0.000 | 0.000 | 0.796 | 0.000 | 0.000 | 0.000 | 0.000 |
| 5th: | 0.181 | 0.000 | 0.437 | 0.000 | 0.655 | 0.000 | -0.271 | 0.000 |
| 6th: | 0.000 | 0.355 | 0.000 | 0.000 | 0.000 | 0.858 | 0.000 | 0.000 |
| 7th: | 0.186 | 0.000 | -0.077 | 0.000 | 0.387 | 0.000 | 0.935 | 0.000 |
| 8th: | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.828 |
If this mapping is placed between the sliders and the Walsh coefficients, we have a Walsh approximation to traditional Fourier component harmonics. The Walsh to Sine Map slider inserts that mapping. I made it a slider to see what the effect would look if it was done gradually.
Analysis
The Walsh number here is roughly equivalent to the harmonic number. Walsh number N has N pulses distributed over the course of the cycle.
W1 is a 50% duty cycle square wave at the fundamental frequency. W2, W4, and W8 are square waves at one, two, and three octaves above.
That alone is interesting, as timbre design goes, as square waves are all odd harmonics, and the octave square waves are all positioned over otherwise empty space. You can balance odd and even harmonics by mixing these.
You can make stairstep approximations to a sawtooth wave by equal amounts W1, W2, W4, and W8.
The remaining Walsh functions have unequal pulse widths, so each of those contributes more complex patterns of harmonics.
W3 is odd harmonics, primarily 3rd. If you mix in a little fundamental, you can remove some of them, leaving an interesting harmonic pattern.
W5 is similarly odd harmonics, primarily 5th, and widely spread. If you mix in some W3, the timbre changes dramatically.
W6 is alternate even harmonics: 2, 6, 10, 14, 18, 22, and so forth. If you mix in some W2 you can cancel out alternate pairs of those... leaving harmonics 6, 10, 22, 26, etc. Wild stuff.
W7 is a lot of odd harmonics, primarily the 7th. You can mix in some W5 and see interesting changes.
And you can approximate a sine wave by mixing W1: 75, W3: -95, W5: -33, and W7: -100, weighted, although it leaves behind a weird pair of 15th and 17th harmonics.
And you get a double up/down impulse by setting the sliders to W1: 10, W2: 20, W3: 30, W4: 40, W5: 50, W6: 60, W7: 70, and W8: 80. (Weighted.) And then you can invert some of them to create interesting patterns of pulses.
The interractions are interesting. Obviously W1, W2, W4, and W8 don't interract with each other. W1, W3, W5, and W7 include a fundamental component; the others do not. W3, W5, and W7 interract a lot, with large timbral changes.
I started this with skepticism. I never found Walsh functions all that attractive. They are not organic, there is no natural process that operates like them, it's not easy to keep a mental model in your head, and some of the behavior is unexpected. And flat waveforms, like the square wave, in general, do not respond well to subtle phase or frequency modulation.
But maybe there is something here.
Organs
There are some interesting parallels to traditional electronic organs. You can think of the Walsh coefficients as the drawbars on a Hammond organ. There are several major differences. The primary pitches are different, although it would be entirely possible to do a set of Walsh functions whose primary pitches match the Hammond drawbars. Secondly, the Hammond drawbars don't interract, while some fraction of these Walsh functions interract. And third, these drawbars are bipolar with a center zero.
Many non-Hammond electronic organs use a "top-octave generator" circuit to provide the pitches for the top octave, and use flip-flops to divide down the octaves. That leaves square waves for all the notes, so many electronic organ makes add in the octave square waves to approximate a sawtooth. That's the same as we did above, mixing W1, W2, W4, and W8 to approximate a sawtooth. So it would be easy to extend electronic organ divide technology to encompass Walsh Functions.
Summary
So I think this is very interesting and has a lot of potential. My main concern is that the relationship between the sliders and the timbre is not very intuitive.
References
Benjamin Jacoby, Walsh Functions: A Digital Fourier Series
Bernie Hutchins, Experimental Electronic Music Devices Employing Walsh Functions , Journal of the Audio Engineering Society, Oct 1973.
Joseph Walsh, A Closed Set of Normal Orthogonal Functions, American Journal of Mathematics, 1923